Benford's Law Tests for Wikileaks Data

In my first post on the WL Afghanistan data I provided a very high-level view of the data, and found that it generally met expectations for frequency given its context and presumed data generating process. Next, I will look a bit deeper at this process and test if the observed frequencies of reports have properties consistent with a natural data generating process. I will be using Benford's Law to test if the leading digit of weekly report counts follow's Benford's distribution. Benford's Law is often used to test for fraud or tampering in count data. In fact, two professor's in the Politics department at NYU used the test to uncover fraud in the 2009 Iranian presidential election.

Rather than vote counts, however, I will be counting the number of reports observed every week in the data set, which amounts to 318 weeks of count data. This is of particular interest to this data because we may be able to provide evidence that the data were altered from their original collection. After the jump is a visualization of this test for the total data set, but before proceeding there are two important things to keep in mind. First, this is not the most straightforward application of Benford's Law, as the data had to be compacted and counted to get into a suitable form (e.g., split into weeks, etc.). Second, given that these date are leaked intelligence reports, we should expect there to be so degree of selection, but the test is not able to show where that selection occurred—only that it did.

Using the weekly time-slices as counts, plots shows some tampering or selection may have occurred. The Pr(1) in the observed data set is much lower than the theoretical expectation provided by Benford, and moving forward along the x-axis the observed data slowly return to the theoretical expectation. Also, as suggested in the comments, I used a chi-square goodness-of-fit test to see if the deviation is statistically significant, but it was not; with a p-value of 0.2303. Meaning we would fail to reject the null hypothesis: the observed data were a good fit for a Benford process. That said, the p-value is not so large as to suggest total adherence.

Also, the above analysis does not provide insight into where that deviation occurs within the data. Also, One way to investigate the later question would be to split the data out by region, and then re-run the test. This might help isolate where the tampering occurred, as would be the case if the test were being applied to vote counts by precinct, etc. Below is a visualization of this more detailed test.

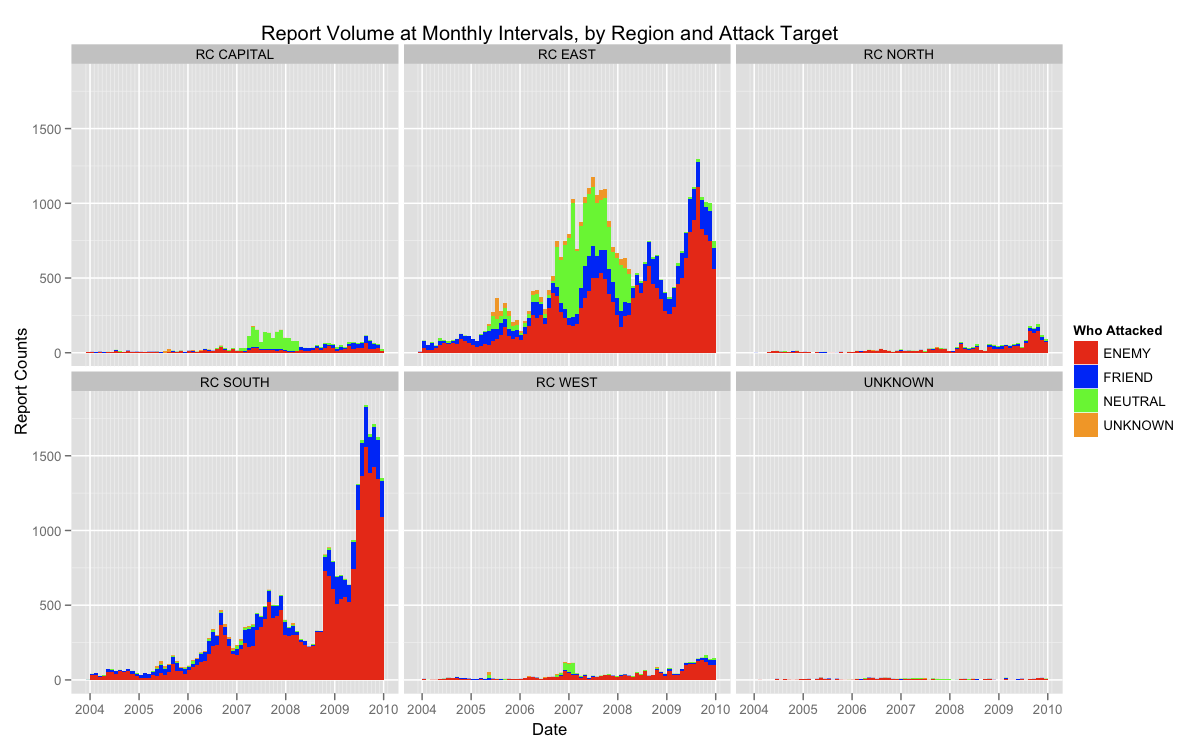
This test is much more revealing. Here we can see that many of the regions follow Benford's law very closely—particularly RC SOUTH and RC WEST. There are, however, slight deviations in the RC EAST and UNKNOWN. Though not nearly as strong a deviation as the total set, the observation from RC is interesting given that we know from the previous analysis that this is also the area with the heaviest reporting volume. The chi-square test for these data also reject the null hypothesis.

Overall, this test does not provide strong evidence for tampering with the data, but it does indicate that some may have occurred, perhaps disproportionately in data from RC EAST. Finally, I have opened a Git repository for this analysis, so you may go there to see how these (and previous/future) analyses were performed.

Wikileaks Afghanistan Data

By now, you have most certainly have read about the publication of a massive (72,000+) number of classified documents related to coalition operation in Afghanistan by the whistleblowers group Wikileaks. The data are available in several formats at the Wikileaks dedicated site.

Before proceeding, I want to point out that given the nature by which this information was obtained and subsequently disseminated I am unclear as to the legal protections provided to those in possession of the data (i.e., retaining copies on their hard drives), or performing analysis (i.e., citing data in research). As such, I am not recommending or condoning anyone download the data until these questions are explicitly addressed.

I, however, have downloaded the data and begun examining it at a high-level. I believe such an examination is critical for two reasons: first, this is the first time in history that the public has been given such a granular view of the day-to-day operation of contemporary warfare. With the proper analytical tools, this data may reveal insights to the predicates of conflict in ways that previous aggregate-level data could not. Second, because the data may have gone through some degree of filtering/selection by Wikileaks, an intricate analysis of the data may provide insight into the nature of that selection and the process by which this selection occurred.

After the jump is an initial overall descriptive visualization of the data as it was provided by Wikileaks, with some brief interpretations. Over the next several days and weeks, I hope to examine the data in more detail and periodically present the results.

The above graph displays the volume of reports over the six year period covered by the data set, broken down by the reporting region, e.g, RC SOUTH, RC EAST, etc.; and the target of attack noted in the incident report, e.g., ENEMY, FRIENDLY, etc.

My motivation in creating this chart was to do a very quick assessment of the trends in the data. Given the nature of the reports, we would expect a noticeable degree of seasonality (peaks and valleys) given the natural ebb and flow of war. Any drastic deviations from this expectation could indicate a strong degree of selection on the part of Wikileaks. As you can see, however, the data generally do fit this expectation. Note the dramatic upward trending seasonality present in the heavy reporting areas of RC EAST and RC SOUTH. Perhaps more interestingly, though, is the sudden increase in the number of NEUTRAL reports present in the data for RC EAST and RC CAPITAL for the period roughly between mid-2006 and mid-2008.

Perhaps a more detailed reading of the reports from those areas at that time would reveal information about the nature of the fighting at that time, or the selection process present in the data.

What Will 'Data Science' Teach Us?

If the level of online discourse is a good indicator of whether a topic has penetrated the collective nerd consciousness, then the notion of a burgeoning "data science" discipline has taken hold. A few weeks ago I discussed where to draw the line on this idea, but recently I again begann thinking about the idea and term more critically. Yesterday, I had a wonderful discussion with a brilliant member of the data community here in New York, which focused on the delicate balance between keeping a human-friendly face on mass quantities of data—something the data scientists are meant to do—and having this new discipline make formidable contributions to our general understand of human behavior.

That is, up to this point, many of the great evangelists of data science have focused on telling stories with data. Science, however, is not about story telling, but about discovery. Perhaps I am particularly cautious of the suffix "science" because of the awkward self-consciousness the word has imbued in my own discipline. At its roots, political science was a discipline that sought to construct narratives; equal parts history, philosophy and personal experience. The name "political science," therefore, brought the ire of the "hard science" community, as they felt (perhaps with reason) that the word had been appended to the title erroneously, as there were no identifiably scientific aspects to the endeavor. While my discipline has come a long way in its application of the scientific method, and today can much more accurately be referred to as a science, there continues to be a delicate balance between discovery and story telling. What, then, can the data science community learn from this experience?

Broadly, all disciplines are measured by their contributions to our understanding of the universe. Data science—by design—is the product of measured human activity, and therefore should seek to provide new insight into human behavior. Unfortunately, the current focus of many of the community's members has been a self-congratulatory appraisal of the tools that have been developed to allow for this large-scale measurement and recording. To be a successful discipline, however, the focus must move away from tools and toward questions.

To paraphrase a famous nerd, with great data comes great responsibility; so to begin, the data science community must ask: what questions do mass quantities of measured human existence allow us to address that were never previously possible? Just the thought should be enough to inspire some to begin writing research proposal, but in effort to contribute to this discussion here are a few things I hope data science will teach us:

• How do online discourses manifest in offline behavior? - I study terrorism, and one lingering problem in this area is the threat from so-called online radicalization. That is, to what extent does information obtained online influence individuals to join radical organization or commit acts of terror? This question, however, applies to many other areas, such as voting and purchasing decisions. As our ability to analyze these discourses increases, perhaps data science will provide some answers.
• How do we reach the "tipping point"? - Malcom Gladwell did well to introduce the idea of the tipping point, but since then we have learned too little about how these culminations occur, and what—if any—are the consistent behavioral features that lead to them. Often, these events occur online, where data science may be able to analyze the tracks that lead to these phase shifts.
• What are the ethical limits of personal data analysis? - The rise of massive stores of personal data online has been a boon to the data science community, but it has not come without some trepidation. With intimate knowledge of the tools and processes used to capture and analyze this information, this community is uniquely positioned to contribute to a discussion of the ethical limits of their own work.
• Do we really consumer things differently? - Everyday people make decisions about what they will consume; in terms of purchases, food, information, etc., and conventional wisdom states that these decisions are largely a function of birth cohorts, geography, educations, etc. Is this really case? The vast amount of consummatory data being generated online may be able to help us understand the most significant indicators of these differences.
• Can more/better data explain rational irrationality? - Today we learned some of the limits of behavioral economics, which have helped explain instances of seemingly irrational behavior. As the op-ed points out, however, there continue to be many questions that discipline fails to explain. Perhaps, then, the explanations of these anomalies can be borne out of data.

I welcome your own thoughts on what data science will teach us, and hope you will share them. Personally, I think this discipline has the potential to generate vast amounts of knowledge, but must be cautious to not loose sight of the question in the sea of information.

Ten Reasons Why Grad Students Should Blog

Tomorrow is the two year anniversary of ZIA. In keeping with the tradition started last year there are some changes afoot for the website itself, but I will keep those under wraps until the actual birthday (wouldn't want to open your gift early, yes?). Rather, today I would like to be more reflective. A few days ago, as the two year anniversary approached, I began thinking back on not just what I accomplished this year at ZIA but also how much the blog has provided me. Upon this reflection it occurred to me that this endeavor has been incredibly beneficial. As such, it seemed logical to me that this would also be the case for many other grad students; which was immediately triggered the question: then why do so few do it?

There are a few notable exceptions, but for the most part it is the faculty that partake in blogging. Perhaps this is simply a function of my particular discipline, in which I—admittedly—do most of my blog reading. I have, however, been to many corners of the blogosphere, and at least within my N=1 sample this appears to be a common phenomenon. I welcome others to show me that this is not the case in other disciplines, but even so, more grad students should be publishing online.

As I thought longer about the vacant state of grad student blogging I wondered if it could be explained as a "they don't know what they don't know" situation. Perhaps by standing from the outside looking in, my fellow grad students simply do not know all of the benefits that can come from participating in an online discourse. To remedy this informational problem, and in an attempt to encourage more grad students to begin blogging, I present (in no particular order) my ten reasons why grad students should blog:

1. You actually have something to say - This is perhaps the best reason why you should be blogging. One of the most frustrating characteristics of the blogosphere is its inherent infinitesimal signal-to-noise ratio. As a grad student, especially those in PhD programs, you have already been deemed qualified to participate in the discussion at a very high level by a panel of distinguished scholars, i.e., the admission committee. Why keep all that smart analysis to yourself?
2. Honing your craft - At its core, graduate school is preparing you to be an active member of the academy. While we may struggle through our preliminary methods classes as we build our technical expertise, it is the application of these tools to interesting research questions that builds successful careers. A blog provides a wonderful lab for experimentation, both in terms of the technical application of methods and toying with research questions in sub-fields of your discipline you may not have otherwise tested.
3. Establishing an identity - If you are in graduate school to be the "best kept secret in academia," you are making a fatal mistake. As with any other job market, getting the preverbal foot in the door for a job talk at a university is a critical first step. As a graduate student it can be incredibly difficult to navigate the sea of senior faculty, their research agendas, and how that fits into your career goals. Having a blog provides you an independent beacon upon which you can broadcast your own ideas. Consider this, ZIA is but a tiny blip within the academic blogosphere, but in the last year my CV has been downloaded by over 875 unique visitors, or more than twice a day.
4. Extending your network outside of academia - Though it is often hard to imagine this from within the cozy confines of the ivory tower, there are a lot of brilliant people outside of academia interested in exactly the same things you are. The difficulty, however, is connecting with them. The Internet is a powerful networking device, and if you are willing to put yourself out there these people will seek you out (Kevin Costner knows what I am talking about). Your bonafides are already largely taken care of (see point reason #1), now you have to impress the Internet with your brilliant musings.
5. The faculty in your department will not think less of you - I have been asked several times by fellow grad students some form of the following question: "Weren't you worried what your advisors would think about your blog?" Of course, I never even thought about this question, as I started blogging before actually matriculating to NYU (note that ZIA's anniversary is early-June and most universities begin the Fall semester in late August). This, however, is besides the point. No, I was never worried about what my advisors would think. The things I write about on ZIA are exactly the same kinds of things I say in seminar and write for term papers (in fact, these ideas often flow both ways). Furthermore, most of those faculty who might actually view blogging in a negative light are also those most unlikely to ever read your blog.
6. Instant and broad criticism of your work - Part of the maturation process for any grad student is developing the ability to receive, absorb, and convert criticism. Much of this will come from rote academic traditions contained within the classroom and conferences, but a blog offers an alternative channel for this criticism. Not only will you get criticism from fellow academics, but criticism from non-academics can illuminate aspects of your research that can be improved to allow for broader understanding.
7. Sharpening your own critical eye - What is the primary thrust of most graduate seminars? Read a series of papers, and spend the next 120 or so minutes tearing them apart. This is meant to help students recognize the difference between good and great work, but also begin to discover where the more fertile patches exist within the landscape of possible research agenda. There are, however, many more papers published in a semester than any one seminar could possibly hope to cover. Also, many seminars are focused on seminal works, not cutting edge research—the same cutting edge research you are most likely already reading in your free time. A blog provides you a platform upon which to criticize this new work, and if you are very lucky (as I have been on a few occasions) an opportunity to interact with the authors in a public forum.
8. Oh, the places you'll go - A combined effect of reasons #1-5 is you will be given the opportunity to travel all over the world and participate in many conferences, seminars, panels, etc. Without a public voice on the Internet I would have never had the opportunity to present to the Bay Area R User's Group or the University of Michigan's Center for the Study of Complex Systems. As you extend your network outside of academia it will take you to places you could never have thought possible without the blog.
9. Building technical expertise - Not all of the work you put into your blog will go toward writing noteworthy posts. Some of the effort, particularly at the outset, will be focused on building the actual site. This will require you to learn technical skills you would have otherwise never had the need or desire to. This is incredibly useful in and of itself, but these skills can be applied beyond blogging. Considering how charts from a paper will look in the online version of your paper (the version most readers will see) is something you may only have thought of after several iterations of trial and error posting it to your blog.
10. It is just plain fun - You are a nerd. You enjoy writing. In many ways, a blog sells itself. But, the additional joy you will feel as you watch your daily hits go up, and the frequency of (non-SPAM) comments increases, will become a powerful motivating force in your day-to-day. A wonderful side effect of which is that the overall quality of your work will also increase, as you become a better writer, researcher and conveyer of complex ideas.

I realize that this will not motivate everyone to navigate over to WordPress and being their own blogs, but I hope it has helped you understand some of the benefits of having your own presence on the Web. I welcome your own thoughts, either as a grad student blogger, or as someone unmoved by the above reasons.

Where to Draw the Line on 'Data Science'?

I completely agree with Tim O'Reilly. Mike Loukides' post on what is data science is a, "seminal, important post." If it has managed to avoid your gaze over the past twenty-four hours I highly recommend it; if nothing else, it is a 2,000 word massage of the data geek ego and a nifty tool and who's who reference to boot. As the latest in a recent series of blog post and magazine/newspaper articles on the rise of the data scientist Loukides draws broad strokes on this emerging discipline, covering everything from where the data comes from, to how to manage it, and who is doing great work (kudos for getting quotes for so many excellent members of the data community).

While I think it is important to write and discuss the importance of this field, I think it is equally important that we—the data science community—do not fall into a perpetual cycle of self-admiration and navel gazing. That is, when asking the question, "what is data science," we should also be asking, "what is not data science?" Or, perhaps more appropriately, "What is good data science, and how do I become a good data scientist?" These questions have not been the focus of the discussion thus far, and it is time to start asking them.

Up to this point the discussion of what is data science has been rather inclusive. As Loukides notes:

In the last few years, there has been an explosion in the amount of data that's available. Whether we're talking about web server logs, tweet streams, online transaction records, "citizen science," data from sensors, government data, or some other source, the problem isn't finding data, it's figuring out what to do with it.

After reading the Loukides piece in the context of what has already been said, I was struck by what appears to be a gradual blurring between what is science and what now being promoted as data science. As an example, consider the recent adjustment of the estimated amount of oil spilled into the Gulf coast. Using the live video feeds of the spill and satellite imagery, FSU oceanographer Ian R. MacDonald performed "rough calculations" to find that the actual amount of oil being spilled may have been four or five times what the government had estimated. Now, were the calculations performed by Dr. MacDonald data science, or just science? His data came from the streaming ethers of the Internet pointed out by Loukides and others; the external spring from which data science flows, but his primary tools were his own eyes and decades of experience.

Before you accuse me of pedantic folly, my purpose with the MacDonald example is to highlight the fact that good data science is exactly the same good science. The most meaningful analyses will be borne from a thorough understanding of the data's context, and an acute sense of what the most important questions should be asked. The conversation up to this point, unfortunately, has been far too focused on the data resources themselves and the tools used to approach them. Good data science will never be measured by the terabytes in your Cassandra database, the number of EC2 nodes your jobs is using, or the volume of mappers you can send through a Hadoop instance. Having a lot of data does not license you to have a lot to say about it.

To that end, I have been disappointed in the lack of mention as to on how critical the social sciences are to good data science. Loukides quotes LinkedIn's Chief Scientist DJ Patil in reference to who makes the best data scientist:

...the best data scientists tend to be "hard scientists," particularly physicists, rather than computer science majors. Physicists have a strong mathematical background, computing skills, and come from a discipline in which survival depends on getting the most from the data.

While I have the upmost respect for physicist, like Patil, their discipline is unencumbered by such pesky matters as human free will and fallibility. I happen to know that DJ respects and understands the difference because I have had the great pleasure of discussing this issues with him, but imagine how much more difficult the so-called hard sciences would be if atoms got to decide their own charge? As data science is fundamentally about gleaning information from the data trail of humans those with perspective on causality in this context are invaluable. While large data stores may be interested in running a regression over some set of variables, a good data scientist would first wonder what the underlying process was that generated those observations, what is missing, and how that affects the interpretations of results.

My assessment of the current state of data science is best described as cautious optimism. The tools needed to capture the data deluge (as Chris Anderson puts it) have developed at a truly astonishing rate. And though I think those leading the data science charge are brilliant and preeminently capable of continuing its surge; I fear our intuitions about what the data mean have not kept pace, and it may be sooner than later that our analyses suffer for it.